А.В. Воробьёв, И.С. Колемасов, В.Г. Финагин

В гуманитарной и естественно-научных сферах перед исследователем особо остро встаёт проблема математического подтверждения той или иной гипотезы. Дело в том, что вследствие специфики предмета исследования часто возникает необходимость оперирования так называемыми латентными (скрытыми) переменными, что делает невозможным проведения их непосредственного измерения.

Рассматривая проблему с осанкой, в настоящее время, к сожалению, часто встречаемую у детей и подростков, важно определиться с природой её происхождения, что в значительной степени будет влиять на формирование подходов к её эффективному лечению и профилактике. Результаты последних медицинских и междисциплинарных исследований достаточно убедительно говорят в пользу психосоматической природы данной группы заболеваний. Тем не менее, в любом научном изыскании желательно иметь строгое математическое подтверждение истинности получаемых выводов. В нашем случае ситуация осложнена характером исходных данных. Так, например, в рассматриваемом далее примере из 11 независимых переменных (на схеме расположены внизу в прямоугольниках) только 2 имеют корреляцию с зависимой переменной (Искривление позвоночника), едва превышающую уровень статистической значимости (р=0,05), а среднее значение их модулей равно 0,06. Дисперсионный анализ групп, разделённых по основанию наличия диагноза, также не даёт статистически значимого различия между ними. Оценка качества регрессионного анализа не оставляет никакой надежд относительно и этого метода.

В данной статье мы расскажем о некоторых математических методах, с помощью которых появляется возможность подтвердить (или опровергнуть) гипотезу исследования в условиях, когда особенности исходных данных делают невозможным использование «стандартного набора» из арсенала исследователя.

Одним из математических методов, способных эффективно справиться с поставленной задачей, мы считаем Структурное моделирование (моделирование структурными уравнениями), которое вобрало в себя большое количество существующих методов статистического анализа данных. Оно наиболее полезно и эффективно в тех случаях, когда внутренняя структура объекта исследования неизвестна, и может только предполагаться исследователем на основе теоретических концепций, а также по некоторым своим проявлениям в виде измеряемых параметров. Основное предназначение метода заключается в том, чтобы проверить, насколько экспериментальные данные совпадают с представлениями учёного. Структурное моделирование позволяет соотносить объективно измеряемые характеристики с гипотетическими (латентными) переменными, введенными в модель исследователем, и выявить силу их взаимосвязей.

На рисунке представлена диаграмма путей, с которой всегда начинается построение структурной модели. Прямоугольниками обозначены явные (измеряемые) переменные, в овалах – неявные (латентные) переменные. Остаточные переменные на диаграмме не обозначены, но в вычислениях участвовали в полном объёме как отражающие специфику переменной. Для произведения расчетов мы воспользовались модулем SEPATH, входящим в состав программы STATISTICA.

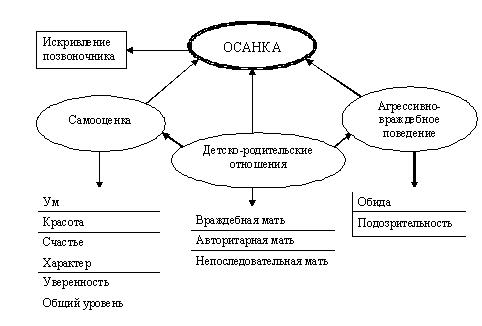
Когда речь идёт о построении математических моделей, включающих латентные переменные, вопрос адекватности модели становится особенно актуальным. Поэтому для оценки результатов структурного моделирования, используется огромное количество параметров. Не имея возможности вдаваться в подробности, заметим, что по совокупности этих параметров адекватность нашей модели можно оценить как «очень хорошую». Кроме того, если в исследовательских целях несколько изменить модель, произведя инверсию казуальности, «перевернув» причинно-следственную связь влияния искривления позвоночника на осанку, то получим столь значительное ухудшение вышеназванных параметров, что адекватность модели становится неудовлетворительной. Это однозначно свидетельствует о том, что структурное моделирование оперирует не просто связями между переменными, а причинно-следственными связями, в отличие от подавляющего большинства других математических методов, включая факторный анализ.

Следующий математический аппарат – Искусственные нейронные сети – мы использовали для непосредственной оценки качества модели, т.к. лучшим показателем истинности продолжает оставаться практика. Нейронные сети хорошо справляются с задачами моделирования сложных многомерных нелинейных зависимостей и могут быть применены для эффективного прогнозирования.

На основе тех же исходных данных с помощью модуля Statistica Neural Network (так же входящего в состав программы STATISTICA), была построена модель в виде трехслойного персептрона (см. рис.), которая позволяет с вероятностью 0,87 (показатель получен на контрольной выборке) спрогнозировать искривление позвоночника у ребёнка на основе всего 11 психологических показателей.

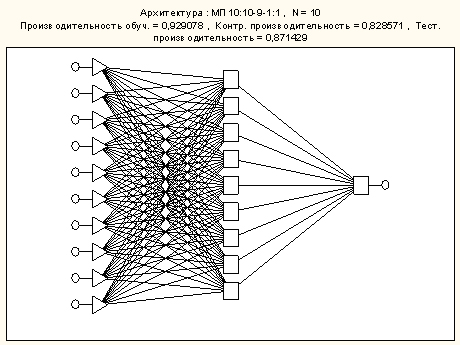
Таким образом, с помощью двух современных методов математического моделирования мы подтвердили гипотезу о психосоматической природе возникновения проблем с осанкой, в частности – искривления позвоночника. Кроме того, мы смогли убедиться в возможности эффективного прогнозирования данного заболевания на основе психологических показателей, что имеет несомненную практическую ценность.

Воробьёв А.В., Колемасов И.С., Финагин В.Г. Математическое подтверждение психосоматической природы возникновения проблем с осанкой // Философские проблемы биологии и медицины: Выпуск 3: Традиции и новации: Сборник материалов 3-й ежегодной научно-практической конференции. – Москва, 2009. – С. 399-402.